第2回 - 2018/10/5
あるサークルでのコンパでの精算処理
前提条件
もし、暗算ができるようなら、それはすばらしい。だけど、普通はできないだろう。そこで、Excelを使うことにする。しかしながら、これをいきなり考えるとえらく大変なことになる。考え方を整理する。当然、方程式を立てる。
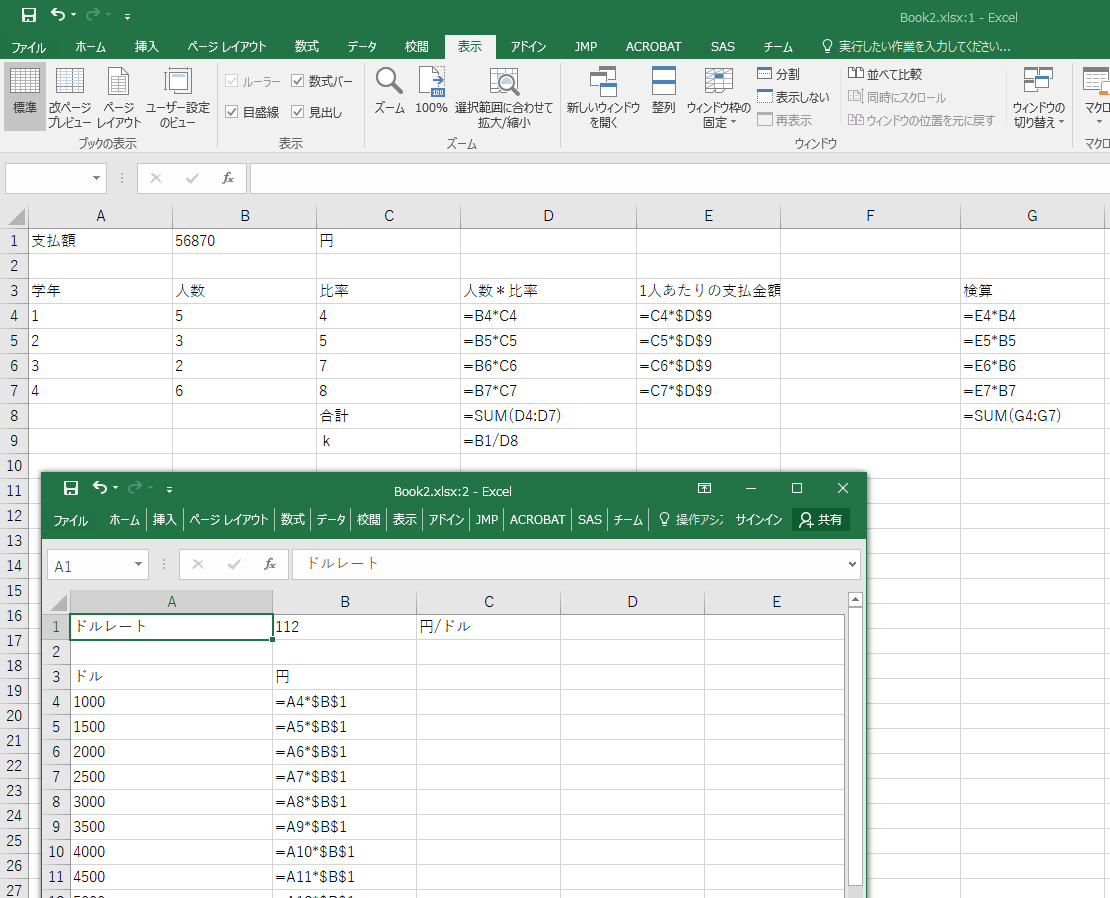
比率の1に対する値をkとする。すると、
すると、s1+s2+s3+s4=56,870だから、まあ、簡単な1次方程式で、kの値は求まり、一人一人の支払額は決まる。だけど、これをワークシートで展開してみる。
中間的に必要な値を考える
実際、どうなったでしょうか?
ワークシートに展開することで

練習問題ごとに新しいワークシートを作り、練習問題番号を、シート名にするといいでしょう。その手の方法で、今回の講義の演習結果を1つのブックファイルにまとめておくと便利だと思います。
A2のセルに、ある果物の1個あたりの重さとして、250(g)を入力します。B2のセルに果物の個数として24を入力します。これらの果物を1つの箱に入れるとします。箱の重さは420(g)だとします。これらの総重量を求める式をC2のセルに入れなさい。
1から10までの数字の合計を求める式を作成してみましょう。(ヒント:1から10までの数値をそれぞれセルに入力して…)
学生仲間4人(それぞれ、A〜Dとする)で、会社を作ることにした。資本金は2000万円とする。均等に割ると500万円だが、社長のAと副社長のBはより多く出資することにした。それぞれの出資比率は4:2:1:1とした。それぞれ、A〜Dの出資金はいくらになるか?
割り勘計算の例をやったが、1円単位を要求する幹事に対して、そんな面倒な支払いやつり銭処理をやってられるか! と非難が集まった。そこで、100円単位になるようにして、支払いをしやすくすることにした。余剰金があれば、じゃんけんで勝った者がもらえ、足りない場合はじゃんけんで負けたものが払うというルールを適用するので、誤差の処理はなんとかなる。後は、金額と誤差を求めることだ。
方針はどうするかを考えよう。本来の支払額を100円単位で四捨五入するのもいいかもしれない。あるいは切り捨てもいいかもしれない。その場合は、足りなくなることは明白だ。
ヒント:四捨五入はROUND関数、切捨てはTRUNC関数を使う(ヘルプで調べよう)
2-1と2-2については、答え合わせはいらないと思います。
Aは1000万円、Bは500万円、CとDは250万円となる。4+2+1+1=8なので、2000万÷8=250万から求められる。これをワークシートに展開するとき、絶対参照と相対参照をうまく組み合わせた式を作り、式を単にコピーするだけでOKとなるように工夫できてればOK。
すでに授業中に作ったワークシートを修正するなどして作業をしますが、シートをコピーして作業すればいいでしょう。
ポイントとなるのは、「きっちりした金額」にするための関数あるいは式をどのように組み立てるかと、それをどこのセルに入れればいいかということです。いろいろ考え方はあるかもしれませんが、いちばん素直なのは、E列の計算結果をさらに切り捨てたり四捨五入するといった処理を加えることです。つまり、E列の式を修正します。100円単位での四捨五入と切り捨ての場合の式は次のようになります。E4のセルの場合だけを示します。
あとは検算結果から差額を求める式をどこかに追加すればいいでしょう。