第11回 - 2018/12/14

相関係数と直線回帰

相関係数とは

対になったデータの関係性を評価する指数で、-1〜+1の間の数値となる。たとえば、

• 身長と体重（1人1人に対して）
• 平均気温とクーラーの売上高（たとえば会計年度ごと）

ただし、無意味な組み合わせを取っても、相関係数は求めることはできる。その場合、まったく無意味な数値なのか、あるいは世紀の大発見か、それはわからない。

• 切手の印刷枚数といわしの総水揚げ量（たとえば、年度ごと）
• 体重と会話速度（1人1人に対して）

数学的な意味では数値は求められるかもしれないけども、意味があるかどうかという議論は、数字を扱う以前の問題である。

相関係数の求め方

公式は次のとおり

• あるデータの組があるとする　{x1, y1} {x2, y2} ... {xn, yn}
• x1, x2, ..., xnの平均値をX、y1, y2,... , ynの平均値をYとする
• 相関係数=Σ（xi-X)(yi-Y) / sqrt(Σ(xi-X)^2 ・ Σ(yi-Y)^2)

実際に相関係数を求めてみる

あまり深い意味はないが、以下のような統計データがある。

日経ナビ2008: 小売業ランキングより

求めるのは、

• 売上高と経常利益
• 売上高の増減率と、経常利益の増減率

の相関係数とする。

ワークシートに計算プロセスを展開して計算をしてみる

実際にやってみます

関数を使った相関係数を求める方法

correl関数を使う　実際にやってみます

分析ツールを使った方法

実際にやってみます

検討

こんな公式も見られる

• x1, x2, ..., xnの平均値をX、標準偏差をS
• y1, y2,... , ynの平均値をY、標準偏差をT
• データの個数をn
• 相関係数=Σ（xi-X)(yi-Y) / (n×S×T)

あるいはこんな公式も

• x1, x2, ..., xnの平均値をX、標本標準偏差をS
• y1, y2,... , ynの平均値をY、標本標準偏差をT
• データの個数をn
• 相関係数=Σ（xi-X)(yi-Y) / ((n-1)×S×T)

実はまったく同じ数値を意味している。

余談

片方の軸が数値ではない場合に相関係数みたいなものを求めたいとする。たとえば、風向きと平均気温の関係のようなもの。あるいは、部屋の壁紙の色と作業効率の関係など。この場合に使われるのが、分散分析。

要因がたくさんあるような測定値から意味のあるものを取り出す処理を因子分析や主成分分析、あるいは多変量解析という。

直線回帰

グラフを描いたとき、そのプロットを平均的に貫く直線があるとする。その直線の式を求める。こうした直線を回帰直線と言う事もあるが、近似直線ということもある。

データとして、x = {x1, x2, ... , xn}、y = {y1,y2, ... , yn}があるとする。

y = ax +b という直線で表現できるとすると、

• b = (n Σ xy - (Σx)(Σy)) / (n Σx^2 - (Σx)^2)
• a = ( (Σx^2) (Σy) - (Σxy) (Σx) ) /  (n Σx^2 - (Σx)^2)

で、定数a、bを求めることができる。実際にやってみます。

元データからグラフを作成する場合は、「散布図」を利用すること。

グラフ上に近似直線を描くことができる。実際にやってみます。

そのほかの方法

SLOPE関数、INTERCEPT関数を使う。

分析ツールの回帰分析（ただし、回帰直線以外のさまざまな情報が得られる）実際にやってみます。

本日の演習

練習問題11-1

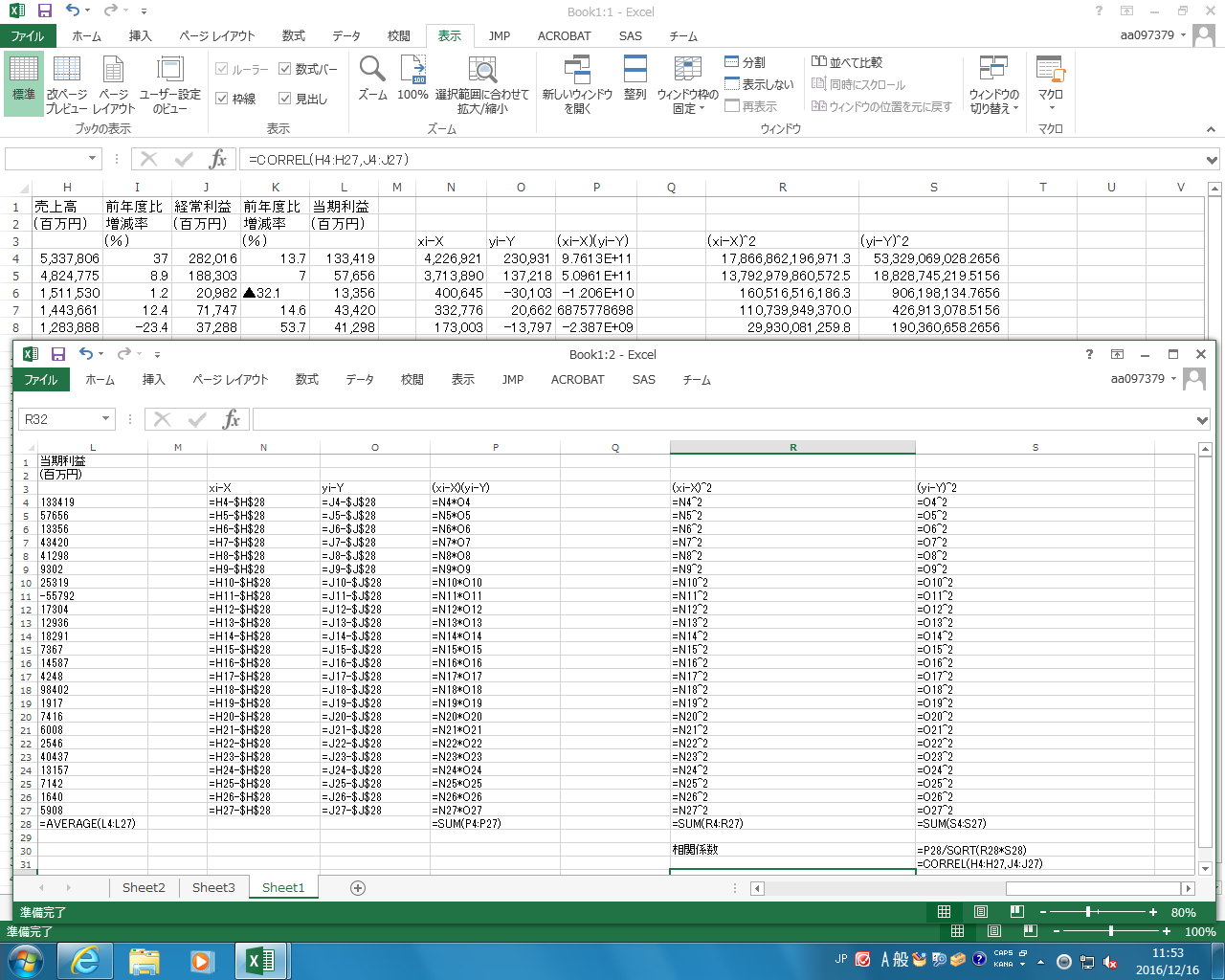
今日のデータのサンプルを利用して相関係数を求める。売上高と当期利益の相関係数を求めてみよう。また、この関係をグラフ（散布図）に描いてみよう。

練習問題11-2

まいどおなじみ日立市の気象と天気予報というページがある。気象観測データというリンクの先に今月の月別データというところがある。適当な月の情報を表示すると、そこには、毎日の平均気温や湿度などが一覧表になっている。

日射量と平均気温の相関係数を求めてみる。散布図も描く。

練習問題11-3

湿度と最大瞬間風速の相関係数を求めてみる。散布図も描く。