第10回 - 2003/12/15

相関係数と直線回帰

相関係数とは

対になったデータの関係性を評価する指数で、-1～+1の間の数値となる。たとえば、

身長と体重（1人1人に対して）
平均気温とクーラーの売上高（たとえば会計年度ごと）

ただし、無意味な組み合わせを取っても、相関係数は求めることはできる。その場合、まったく無意味な数値なのか、あるいは世紀の大発見か、それはわからない。

切手の印刷枚数といわしの総水揚げ量（たとえば、年度ごと）
体重と会話速度（1人1人に対して）

数学的な意味では数値は求められるかもしれないけども、意味があるかどうかという議論は、数字を扱う以前の問題である。

相関係数の求め方

公式は次のとおり

あるデータの組があるとする　{x1, y1} {x2, y2} ... {xn, yn}
x1, x2, ..., xnの平均値をX、y1, y2,... , ynの平均値をYとする
相関係数=Σ（xi-X)(yi-Y) / sqrt(Σ(xi-X)^2 ・ Σ(yi-Y)^2)

実際に相関係数を求めてみる

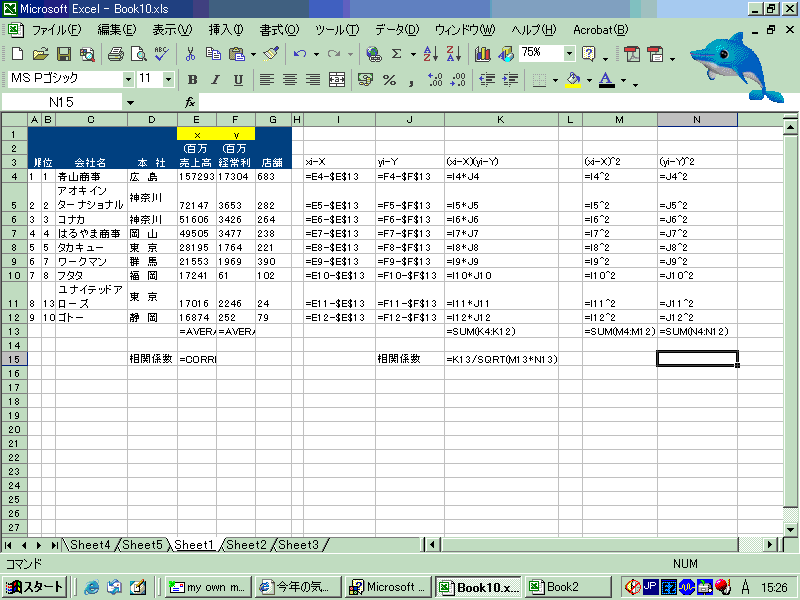
あまり深い意味はないが、以下のような統計データがある。

順位	順前　年位度	会社名	本　社	売上高 (百万円)	伸び率 (％)	経常利益 (百万円)	店舗数
1	1	青山商事	広　島	157,293	▲3.0	17,304	683
2	2	アオキインターナショナル	神奈川	72,147	▲5.3	3,653	282
3	3	コナカ	神奈川	51,606	0.2	3,426	264
4	4	はるやま商事	岡　山	49,505	0	3,477	238
5	5	タカキュー	東　京	28,195	▲12.7	▲1,764	221
6	7	ワークマン	群　馬	21,553	16.7	1,969	390
7	8	フタタ	福　岡	17,241	▲2.0	61	102
8	13	ユナイテッドアローズ	東　京	17,016	18.7	2,246	24
9	10	ゴトー	静　岡	16,874	4.9	252	79
10	6	三峰	東　京	15,926	▲19.5	―	92

専門店売上高ランキングより
http://www.nikkei.co.jp/report/senmon1.html

求めるのは、

売上高と経常利益
店舗数と伸び率

の相関係数とする。

ワークシートに計算プロセスを展開して計算をしてみる

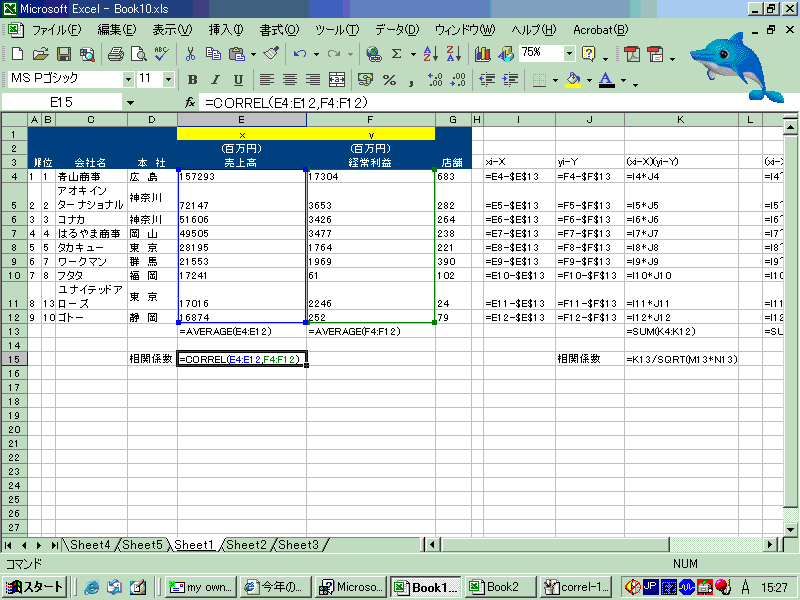
実際にやってみます

関数を使った相関係数を求める方法

correl関数を使う　実際にやってみます

分析ツールを使った方法

実際にやってみます

検討

こんな公式も見られる

x1, x2, ..., xnの平均値をX、標準偏差をS
y1, y2,... , ynの平均値をY、標準偏差をT
データの個数をn
相関係数=Σ（xi-X)(yi-Y) / (n×S×T)

あるいはこんな公式も

x1, x2, ..., xnの平均値をX、標本標準偏差をS
y1, y2,... , ynの平均値をY、標本標準偏差をT
データの個数をn
相関係数=Σ（xi-X)(yi-Y) / ((n-1)×S×T)

実はまったく同じ数値を意味している。

余談

片方の軸が数値ではない場合に相関係数みたいなものを求めたいとする。たとえば、風向きと平均気温の関係のようなもの。あるいは、部屋の壁紙の色と作業効率の関係など。この場合に使われるのが、分散分析。

要因がたくさんあるような測定値から意味のあるものを取り出す処理を因子分析や主成分分析、あるいは多変量解析という。

直線回帰

グラフを描いたとき、そのプロットを平均的に貫く直線があるとする。その直線の式を求める。こうした直線を回帰直線と言う事もあるが、近似直線ということもある。

データとして、x = {x1, x2, ... , xn}、y = {y1,y2, ... , yn}があるとする。

y = ax +b という直線で表現できるとすると、

b = (n Σ xy - (Σx)(Σy)) / (n Σx^2 - (Σx)^2)
a = ( (Σx^2) (Σy) - (Σxy) (Σx) ) / (n Σx^2 - (Σx)^2)

で、定数a、bを求めることができる。実際にやってみます。

元データからグラフを作成する場合は、「散布図」を利用すること。

グラフ上に近似直線を描くことができる。実際にやってみます。

そのほかの方法

SLOPE関数、INTERCEPT関数を使う。

分析ツールの回帰分析（ただし、回帰直線以外のさまざまな情報が得られる）実際にやってみます。

本日の演習

練習問題10-1

今日のデータのサンプルを利用して相関係数を求める。売上高と店舗数の相関係数を求めてみよう。また、この関係をグラフ（散布図）に描いてみよう。

練習問題10-2

まいどおなじみ日立市の気象と天気予報というページがある。気象観測データというリンクの先に今月の月別データというところがある。適当な月の情報を表示すると、そこには、毎日の平均気温や湿度などが一覧表になっている。

日射量と平均気温の相関係数を求めてみる。散布図も描く。

練習問題10-3

湿度と最大瞬間風速の相関係数を求めてみる。散布図も描く。

解答

10-１

相関係数は、correl(E4:E12,H4:H12)で求められる。

グラフは、まず、E3:E12を選択し、続いて、Ctrlキーを押しながらH3:H12を選択する。つまり、不連続領域の選択を行う。その後に、グラフウィザードで、「散布図」を選択すれば、あとはそのまま描けるはず。

凡例は後で消しておけばいい。売り上げと店舗数が比例し、相関係数が高いのは当たり前かもしれない。ワークマンは店舗数の割には売り上げが少ないのに対して、ユナイテッドアローズは逆に店舗数の割には売り上げが大きい、といったことがグラフから読み取れるとなおいいです。

10-2

M5:M6のセル結合を解除しないといけないかもしれませんが、後はさほど難しくないでしょう。B列とM列という不連続な範囲の選択をして、グラフを描きます。もちろん、それが面倒なら、「日平均」「日射量」の列を隣り合わせになるように、表を編集して作業をしてもいいでしょう。

10-3

やり方はもういいかと思いますが・・・。ちなみに、相関係数は負の数になるので、風が強いと湿気は少ないといえなくもないわけですが、ただ、係数自体あまり大きくないので、傾向としては薄いといえるわけです。